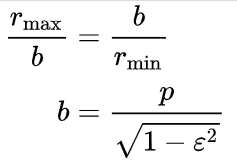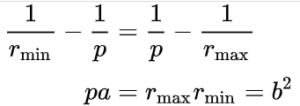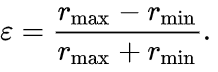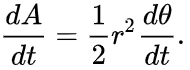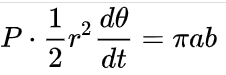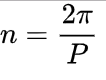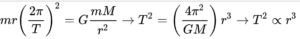Hoy hablaremos sobre las Leyes de Kepler, unas leyes enunciadas para describir matemáticamente el movimiento de los planetas en sus órbitas alrededor del Sol. Les hablaremos sobre la historia, las fórmulas y su nomenclatura, todo lo que te interesa saber, lo encontrarás aquí.
Indice De Contenidos
¿Qué son las Leyes de Kepler?
En astronomía, las leyes del movimiento planetario de Kepler son tres leyes lógicas que describen el movimiento de los planetas alrededor del Sol.
- El círculo de un planeta es un óvalo con el Sol en uno de los dos focos.
- Una sección de línea que une un planeta y el Sol despeja regiones equivalentes en medio de interminables intervalos de tiempo equivalentes.
- El cuadrado del tiempo orbital de un planeta corresponde a la forma tridimensional del pivote semisignificativo de su círculo.
La mayoría de los círculos planetarios son casi redondos, y se requiere una percepción y un cómputo vigilantes con el objetivo final de establecer que no se trata de un círculo vicioso y consumado. Los cálculos del círculo de Marte, cuyas cualidades distribuidas son hasta cierto punto sospechosas, demostraron un círculo. De esto, Johannes Kepler derivó que los diferentes cuerpos del Sistema Solar, incluyendo aquellos más distantes del Sol, tienen además círculos curvos.
La obra de Kepler (distribuida entre 1609 y 1619) realzó la hipótesis heliocéntrica de Nicolaus Copernicus, aclarando cómo se desplazaban las velocidades de los planetas, y utilizando círculos curvos en lugar de círculos redondos con epiciclos. Isaac Newton apareció en 1687 que conexiones como la de Kepler se aplicarían en el Sistema Solar a una suposición decente, como su propio resultado leyes de movimiento y leyes de energía atractiva en general.
Historia
Johannes Kepler distribuyó sus dos leyes iniciales sobre el movimiento planetario en 1609, después de haberlas descubierto examinando las percepciones cósmicas de Tycho Brahe. La tercera ley de Kepler fue distribuida en 1619. Kepler tenía fe en el modelo copernicano del sistema planetario cercano, que requería círculos redondos, pero no podía acomodar las percepciones profundamente exactas de Brahe con un redondeo que encajaba con el círculo de Marte: Marte adventiciosamente tenía el capricho más elevado de todos los planetas, aparte de Mercurio. Su primera ley reflejó esta revelación.

A Newton se le atribuyó la comprensión de que la segunda ley no es extraordinaria para la ley de la atracción del cuadrado inverso, sino que es el resultado de la idea extendida de esa ley; mientras que las leyes alternativas se basan en el tipo de cuadrado opuesto de la fascinación. Carl Runge y Wilhelm Lenz distinguieron mucho más tarde una regla de simetría en el espacio escénico del movimiento planetario (el conjunto simétrico O(4) actuando) que representa la primera y tercera ley a causa de la atractiva energía newtoniana, como lo hace la preservación de la fuerza precisa por medio de la simetría rotacional para la segunda ley.
Fórmulas
El modelo matemático de la cinemática de un planeta sujeto a las leyes permite una amplia gama de cálculos adicionales.
Primera ley de Kepler
La órbita de cada planeta es una elipse con el Sol en uno de los dos focos. Matemáticamente, una elipse puede ser representada por la fórmula:
Dónde está el recto semilato, ε es la excentricidad de la elipse, r es la distancia del Sol al planeta, y θ es el ángulo a la posición actual del planeta desde su aproximación más cercana, vista desde el Sol. Así que (r, θ) son coordenadas polares.
Para una elipse 0 < ε < 1 ; en el caso límite ε = 0, la órbita es un círculo con el sol en el centro (es decir, donde hay cero excentricidad).
En θ = 0°, perihelio, la distancia es mínima.
En θ = 90° y en θ = 270° la distancia es igual a .
En θ = 180°, aphelion, la distancia es máxima (por definición, aphelion es – invariablemente – perihelion más 180°)
El semieje mayor a es la media aritmética entre rmin y rmax:
El eje semimenor b es la media geométrica entre rmin y rmax:
El recto semilato p es la media armónica entre rmin and rmax:
La excentricidad ε es el coeficiente de variación entre rmin and rmax:
El caso especial de un círculo es ε = 0, resultando en r = p = rmin = rmax = a = b y A = πr2.
Segunda ley de Kepler
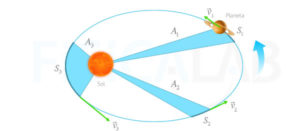
Una línea que une un planeta y el Sol barre áreas iguales durante intervalos de tiempo iguales.
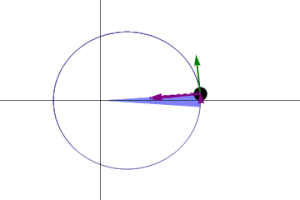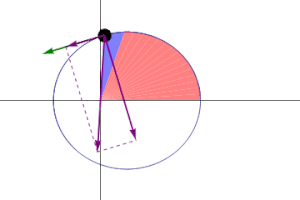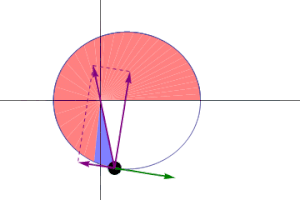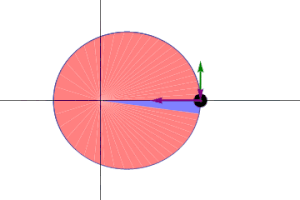
El radio orbital y la velocidad angular del planeta en la órbita elíptica variarán. Esto se muestra en la animación: el planeta viaja más rápido cuando está más cerca del sol, y más despacio cuando está más lejos del sol. La segunda ley de Kepler establece que el sector azul tiene una superficie constante. (Ver: Curiosidades del Planeta Mercurio)
En poco tiempo el planeta barre un pequeño triángulo que tiene la línea de base
y la altura
y el área
y por lo tanto la velocidad de área constante es
El área delimitada por la órbita elíptica es Así que el período
satisface
y el movimiento medio del planeta alrededor del Sol
satisface
Tercera ley de Kepler
Bajo la constante mirada de las leyes de Kepler se redactaron diferentes investigadores, por ejemplo, Claudio Ptolomeo, Nicolás Copérnico y Tycho Brahe, cuyos principales compromisos con el avance de la ciencia fueron haber obtenido estimaciones excepcionalmente exactas de los lugares de planetas y estrellas. Kepler, que era alumno de Tycho Brahe, aprovechó cada una de estas estimaciones para planificar su tercera ley.
Kepler podía retratar el movimiento de los planetas. Utilizó el aprendizaje científico de su oportunidad para descubrir conexiones entre la información de las percepciones cósmicas obtenidas por Tycho Brahe y con ellas descubrió cómo hacer un modelo heliocéntrico del universo. Comenzó a trabajar con el modelo convencional del universo, proponiendo direcciones y desarrollos no convencionales en los epiciclos, sin embargo descubrió que la información de las percepciones lo ponía fuera del plan que Copérnico había construido, lo que lo llevó a inferir que los planetas no representaban un círculo redondo alrededor del Sol.
Intentó diferentes formas para los círculos y descubrió que los planetas representan círculos, que tienen el Sol en uno de sus focos. Desglosando la información de Brahe, Kepler encontró además que la velocidad de los planetas no es constante, pero que el vector de rango que interconecta el Sol (situado en uno de los puntos focales de la dirección curvada) con un planeta dado representa territorios de acercamiento en ocasiones equivalentes. Por lo tanto, la velocidad de los planetas es más notable cuando están cerca del Sol (perihelio) que cuando viajan a través de las zonas más distantes (aphelio). Esto ofrece ascender a las tres Leyes de Kepler del movimiento planetario.
El cuadrado del período orbital de un planeta es directamente proporcional al cubo del eje semimayor de su órbita. Esto captura la relación entre la distancia de los planetas del Sol y sus períodos orbitales. Kepler enunció en 1619 esta tercera ley en un laborioso intento de determinar lo que él consideraba la “música de las esferas” según leyes precisas, y expresarla en términos de notación musical. Así que se le conocía como la ley armónica. Usando la Ley de la gravitación de Newton (publicada en 1687), esta relación se puede encontrar en el caso de una órbita circular estableciendo la fuerza centrípeta igual a la fuerza gravitacional:
Luego, expresando la velocidad angular en términos del período orbital y luego reordenando, encontramos la Tercera Ley de Kepler:
Una derivación más detallada se puede hacer con órbitas elípticas generales, en lugar de círculos, así como orbitar el centro de la masa, en lugar de sólo la masa grande. Esto resulta en el reemplazo de un radio circular, , con el eje semimayor elíptico,
, así como en el reemplazo de la gran masa
por
. Sin embargo, dado que las masas de los planetas son mucho más pequeñas que el sol, esta corrección a menudo se ignora. La fórmula completa correspondiente es:
Donde es la masa del sol,
es la masa del planeta, y
es la constante gravitacional,
es el período orbital y
es el semieje mayor elíptico.
Nomenclatura
La definición actual de la obra de Kepler tardó unos dos siglos en chocar con su forma establecida. Los Eléments de la philosophie de Newton (Elementos de la filosofía de Newton) de Voltaire de 1738 fueron la producción principal para utilizar la expresión de las “leyes”. La Enciclopedia Biográfica de Astrónomos en su artículo sobre Kepler (p. 620) afirma que la redacción de las leyes lógicas para estas revelaciones estaba presente en cualquier caso desde la temporada de José de Lalande. Fue la obra de Robert Small, en un registro de las revelaciones cósmicas de Kepler (1814), la que constituyó el arreglo de tres leyes, al incluir la tercera.
Poca garantía adicional, contra la historia, de que se trataba de leyes de observación, a la luz del pensamiento inductivo. Además, la utilización actual de la “Segunda Ley de Kepler” es un nombre algo equivocado. Kepler tenía dos variantes, relacionadas en un sentido subjetivo: la “ley de remoción” y la “ley del territorio”. La “ley regional” es lo que se convirtió en la Segunda Ley en la disposición de tres; sin embargo, Kepler mismo no la benefició de esa manera. (Ver: Astronomía y astrología)

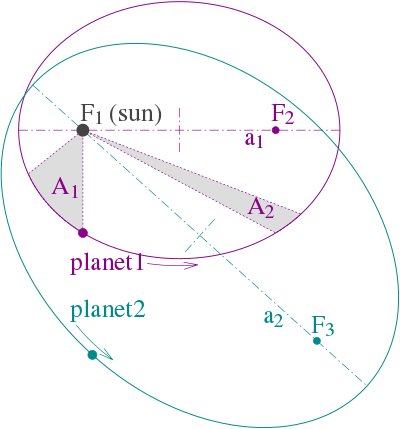
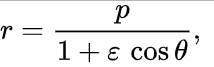
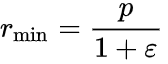
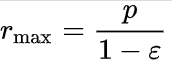
![{\displaystyle {\begin{aligned}r_{\max }-a&=a-r_{\min }\\[3pt]a&={\frac {p}{1-\varepsilon ^{2}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d244bc984688866186efa8db808525b0cc93d55)