Arquímedes, matemático, astrónomo, físico, ingeniero e inventor, Griego. Es considerado uno de los científicos más importantes de la antigüedad, sus aportes son invaluables y se mantienen vigentes hoy en día. Si quieren conocer sobre su vida y las aportaciones de Arquímedes, se encuentran en el artículo indicado.
Indice De Contenidos
Biografía de Arquímedes
Los datos sobre la vida de Arquímedes pueden ser en ocasiones poco confiables, sin embargo, cuando realizas una investigación profunda, puedes identificar que la mayoría de las fuentes coinciden en que Arquímedes nació en Syracusa en el año 287 antes de Cristo. Actualmente es una ciudad capital de Italia, ubicada en la costa sureste de la isla de Sicilia.
Para la época de Arquímedes Syracusa era una colonia Griega, la cual fue fundada por colonos de Corintio en el año 734 antes de Cristo. Existen sugerencias de que en el documento escrito por Arquímedes El Contador de Arena, en la que Arquímedes trata de establecer un límite superior para la cantidad de granos de arena necesarios para llenar el universo, señala el nombre de su padre, quien se llamaba Fidias y era un astrónomo.
La vida de Arquímedes es como armar un gran rompecabezas, ya que vas obteniendo información de su vida de manera dispersa en la literatura. Existe una obra titulada Vidas Paralelas, escrita por Plutarco, en la que señala que Arquímedes era familia de Hierón II de Syracusa, la historia cuenta que era un tirano que gobernó en los años 265 antes de Cristo.
Existen algunos datos que señalan que Arquímedes curso estudio en Alejandría, en Egipto, información que es respaldada, debido a que en los escritos de Arquímedes hace referencia y cita a muchos de los científicos de la ciudad de Alejandría, lo que permite suponer que los conocía y recibió educación de alguno de ellos, en especial de Euclides. También hace referencia a algunos científicos de Alejandría como amigos cercanos. Se dice que Arquímedes falleció a la edad de 75 años.
La ciudad de Syracusa era asediada por los Romanos, sin embargo, lograr el control de la ciudad les llevó más de 2 años de constante lucha. Se dice que Arquímedes falleció precisamente durante la segunda guerra púnica, los Romanos que atacaron la ciudad estaban comandados por Marco Claudio Marcelo, un General romano, muy respetado por su ejército.
Arquímedes falleció a manos de un soldado romano que no atendió las órdenes de Marcelo, quien había ordenado perdonar la vida del reconocido matemático. Existen diversas versiones de la manera en cómo murió Arquímedes, todas llevan al mismo desenlace y también coinciden con la época de la toma de la ciudad de Syracusa.
El General Marcelo, se enfureció con la noticia sobre la muerte de Arquímedes a mano de uno de sus soldados, ya que estaba en conocimiento del valor que tenía Arquímedes. Hay muchos escritos que hacen referencia de la participación de Arquímedes en la defensa de la ciudad, indican que realizaba armas y artefactos que permitían mantener a los Romanos alejados.
Por lo tanto, Marcelo estaba en conciencia del valor que representaba el matemático. No existe ningún escrito o referencia que permita inferir que Arquímedes tuvo esposa e hijos, es posible que los tuviera pero no hay nada que indique que así fuera.
Es poco lo que se sabe de su vida personal, como señalamos al principio lo poco que se sabe hay que hurgar en los escritos de Cicerón, Plutarco y Tito Livio, que tenían en común ser escritores e historiadores, sin embargo, ellos también tenían que investigar sobre la vida de Arquímedes para poder escribir sobre él, y los hallazgos sobre su vida, fueron pocos. En lo que, si hay coincidencia, es que su entrega a las ciencias lo mantenía absorto de acciones básicas para la vida, como comer.
Descubrimientos
Como vemos Arquímedes tenía una capacidad increíble de invención además de ser un hombre con múltiples disciplinas, entre ellas matemática, física, ingeniería y adicionalmente era astrónomo. Adicionalmente, siempre se planteaba la búsqueda de explicaciones a situaciones que los demás ni lo pensaban, entre ellas se encuentra por ejemplo el cálculo del volumen de un cuerpo irregular.
Como podrán imaginar hoy en día y con todos los conocimientos, herramientas y expresiones matemáticas que conocemos, es muy sencillo calcular el volumen de un cuerpo con una forma determinada, por ejemplo, un círculo o un rectángulo.
Sin embargo, sigue siendo todo un artilugio matemático calcularlo para un cuerpo irregular en esta época, ahora solo imaginen hacerlo para un cuerpo irregular en la época de Arquímedes, definitivamente este hombre era un erudito (un hombre con conocimientos muy profundos en muchas áreas).
Entre los descubrimientos reconocidos se encuentra el de la corona dorada, que inició siendo un reto para determinar si en realidad la misma estaba elaborada solo con oro. También se encuentra el famoso Tornillo de Arquímedes y la Garra de Arquímedes. ¿No tienen ni idea de lo que estamos hablando?, entonces los invito a conocer sobre los mayores descubrimientos de Arquímedes, de los cuales comentaremos con detalle a continuación:
La corona dorada
Generalmente Arquímedes se le solicitaban la resolución de problemas a situaciones cotidianas o sus invenciones surgían buscando explicaciones a fenómenos desconocidos que luego resultaban ser de gran ayuda.
La invención del método para calcular el volumen de objeto con forma irregular, surge de la búsqueda para confirmar si una corona que había mandado a elaborar en oro Hieron II, como sabemos era quien gobernaba Syracusa, realmente estaba hecha solo de oro, o el artista orfebre había utilizado otro metal de menor valor como la plata para su elaboración.
Quizás no hubiera sido tan complicado salir de la duda si se tratara de una corona cilíndrica, pero este no era el caso, se trataba de una corona con detalles y formas, porque era una corona triunfal. Como podemos imaginar la vida del orfebre se encontraba en las manos de Arquímedes, así que, si su respuesta o metodología para determinar si era solo de oro, era la equivocada, la muerte de un inocente seria solo su responsabilidad.
Ahora si era la correcta, entonces todo dependería de la honestidad del orfebre. Con esta inmensa responsabilidad en sus manos Arquímedes comienza a analizar la manera de determinar de qué estaba elaborada la corona. Además de ello, debía resolver el problema sin dañar la corona, por lo tanto, no podía fundirla, lo cual hubiera sido una solución sencilla, ya que solo debía convertirla en un cuerpo con forma regular y calcular su masa y volumen y con esta información determinaría su densidad.
Luego de pensar durante todo el día sin encontrar solución al problema, decide tomar un baño. En la época las duchas se tomaban en sendas poncheras o barriles de madera que se llenaban de agua y las personas se metían en ellas para bañarse.
Pues Arquímedes al darse un baño se da cuenta que, al entrar en la bañera, el nivel del agua de la misma subía, en ese momento surge entonces la idea, que ese podría ser el método para determinar el verdadero volumen de la corona. ¿Pero cómo sería esto posible?, pues sencillo para nosotros actualmente que tenemos el conocimiento que en su momento descubrió Arquímedes.
Como el agua no comprimiría, ni cambiaría la forma de la corona de oro, al colocar la misma en un recipiente con un volumen de agua conocido, cuando se coloca la corona dentro, se desplazará una cantidad de agua que será igual al volumen de la corona. Conociendo entonces el peso de la corona y el volumen de la corona a través del agua desplazada, podía conocer su densidad, con solo dividir el peso entre el volumen.
Si el orfebre hubiese utilizado otros metales diferentes del oro, la densidad de la corona sería menor que la densidad del oro. Eureka!! Tenía en sus manos la solución que demostraría la honestidad o no del orfebre. Cuentan que la reacción de Arquímedes fue salir corriendo a la calle emocionado por haber encontrado la solución al problema, pero olvido un pequeño detalle, Arquímedes olvido que se estaba bañando y salió a la calle sin vestirse.
Este descubrimiento de Arquímedes no se encuentra documentado en sus trabajos, existen investigadores que dudan que en realidad Arquímedes haya encontrada la solución utilizando este método, porque consideran que era sumamente impreciso la manera en cómo mediaría el volumen de agua desplazada por la corona.
No obstante, sugieren que es posible que Arquímedes haya utilizado el principio de la hidrostática, el cual había sido descrito por Arquímedes y se encuentra documentado en el libro que describe el comportamiento de los cuerpos flotantes.
El principio de los cuerpos flotantes sugiere que todo cuerpo sumergido en un fluido va a experimentar una fuerza que lo empujará hacia arriba y esta será igual al peso del fluido desalojado. De utilizar este principio, también es posible comparar la densidad de la corona dorada de Hieron II, al contrastar con un trozo de oro puro y utilizando una balanza.
Al colocar en un lado de la balanza la corona dorada, que es de quien necesitaba conocer la densidad y en el otro una muestra de oro puro del mismo peso del cual por supuesto ya conoce la densidad, porque sabe que es una muestra pura, procedería a sumergir la balanza en el agua; si la corona estuviera elaborada con otros metales a parte del oro, tendría menos densidad que el oro, desplazaría más agua, ya que presentaría mayor volumen, por lo tanto, experimentaría un mayor empuje que la muestra de oro puro.
Galileo Galilei (gran científico Italiano) es de los que expresa que es muy probable que Arquímedes utilizara este método, por ser un método más exacto y que además está fundamentado en descubrimientos y demostraciones documentadas por Arquímedes. También con base en la credibilidad de los descubrimientos realizados por Arquímedes, Galileo Galilei en el año 1.586 creó una balanza hidrostática que servía para pesar metales en el agua y en el aire, por supuesto que utilizando los principios documentados por Arquímedes.
El Siracusia y el tornillo de Arquímedes
Como hemos señalado anteriormente los trabajos, invenciones y descubrimiento de Arquímedes en la mayoría de los casos buscaba entender los procesos de la naturaleza y solucionar problemas de la vida diaria. Y precisamente en esa búsqueda de soluciones realizó grandes invenciones en el área de ingeniería.
Hieron II siempre le realizaba solicitudes a Arquímedes, ya que estaba consciente de la genialidad de este increíble científico. Es así que los documentos de Náucratis, quien era un escritor e historiador Griego, plasmo con detalle sobre el barco que Hieron II había solicitado a Arquímedes, por su puesto dentro de las características se había solicitado que el mismo debía ser imponente, grande, capaz de navegar grandes distancias, lujoso, cómodo y servir para la guerra.
Arquímedes puso manos a la obra haciendo los gráficos para la construcción del inmenso barco, el cual fue construido por Arquias de Corinto, quien era un arquitecto Griego, natural por supuesto de Corinto, quien llegó a Syracusa a solicitud de Hierón, rey de Sicilia. Arquias sobresalía en la construcción naval y a pesar de ello, el trabajo de la construcción del barco diseñado por Arquímedes fue supervisado por este.
Lo llamaron en principio el Syracusia, el barco cumplía con todo lo solicitado por Hieron II, luego el nombre del barco fue cambiado por el de Alejandría, ya que fue enviado como regalo al rey Ptolomeo III de Egipto.
Los registros indican que el Syracusia fue el barco más grande de la antigüedad clásica. Dentro de las características más ostentosas que tenía el barco se dice que habían jardines decorativos, un templo dedicado a la Diosa Afrodita, tenía un gimnasio y capacidad para más de 600 personas.
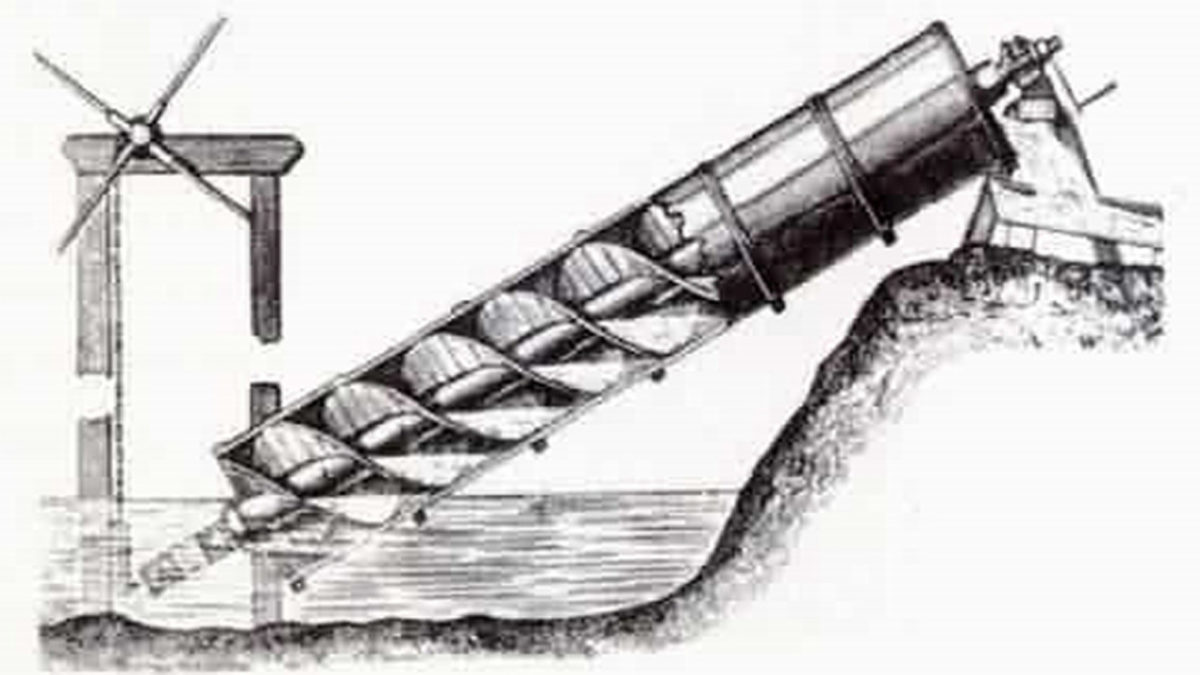
Solo hay que imaginar en esa época un barco con ese tamaño iba a presentar problemas de flotabilidad debido a que entraría gran cantidad de agua en el casco, la cual no podría ser desalojada en el tiempo suficiente para que no se hundiera. Sin embargo, hasta en eso pensó Arquímedes, y allí surgió otro de sus grandes inventos, el cual está vigente en nuestros días y se utiliza en muchos equipos y herramientas, el famoso tornillo de Arquímedes.
Creó un tornillo que permitía sacar el agua de la sentina. El mismo se trataba de un mecanismo que tenía una hoja con forma de tornillo el cual estaba colocado dentro de un cilindro, el mismo se hacía girar a mano y permitía transferir el agua de un lugar a otro.
También fue utilizada esta invención para transferir agua de lugares de aguas bajas hacia canales de irrigación más altos. El tornillo de Arquímedes es muy utilizado en las industrias de cereales y minería para transferir el material de un lugar a otro. Es quizás este invento de Arquímedes el que permitió regar los jardines Colgantes de Babilonia.
La garra de Arquímedes
Ahora comentaremos un poco sobre la Garra de Arquímedes, esta información logró ser obtenida de los escritos de Polibio, un historiador Griego, de quien se dice fue el primero en escribir sobre historia universal. En los documentos de Polibio comenta esta invención de Arquímedes, asociada a uno de los ataques Romanos a la ciudad de Syracusa.
Comenta con claridad de los inventos de Arquímedes para la defensa de la ciudad, los cuales lograron quebrantar la moral del ejército Romano, al punto de pensar que no podrían nunca tomar la ciudad de Syracusa, al menos no por asalto.
Es por ello, que los Romanos tuvieron que cambiar la estrategia de ataque. La ciudad se había defendido utilizando catapultas, escorpiones, grúas, pero hay una llamada manus ferrea, que se le atribuye su invención a Arquímedes. Esta garra consistía en un gancho como el que utilizan las grúas y un sistema de poleas. Ahora detallaremos de qué se trataba este equipo de defensa para la guerra.
Los Romanos llegaban en sus barcos lo más cerca posible de los muros de la ciudad, con la intención de colocar escaleras, que les permitieran subir y tomar por asalto la ciudad de Syracusa, no olvidemos que era una ciudad portuaria.
Pero cuando los barcos Romanos llegaban a ponerse en posición les era lanzada la garra, esta estaba unida a un enorme brazo de madera. Cuando la dejaban caer sobre el barco, por inercia se balanceaba hacia arriba y levantaba la proa de los barcos.
El ángulo al levantar la proa era tal, que provocaba la entrada de agua por la popa. Al estar enganchado, accionaban el sistema de poleas, cuerdas y cadenas, con las cuales subían el barco y lo dejaban caer, produciendo grandes daños a los barcos que llevaban en muchas oportunidades a su hundimiento. Los inventos y armas creadas por Arquímedes han sido puesta a prueba para confirmar su viabilidad y la Garra fue comprobada, siendo un arma de guerra factible.
El rayo de calor
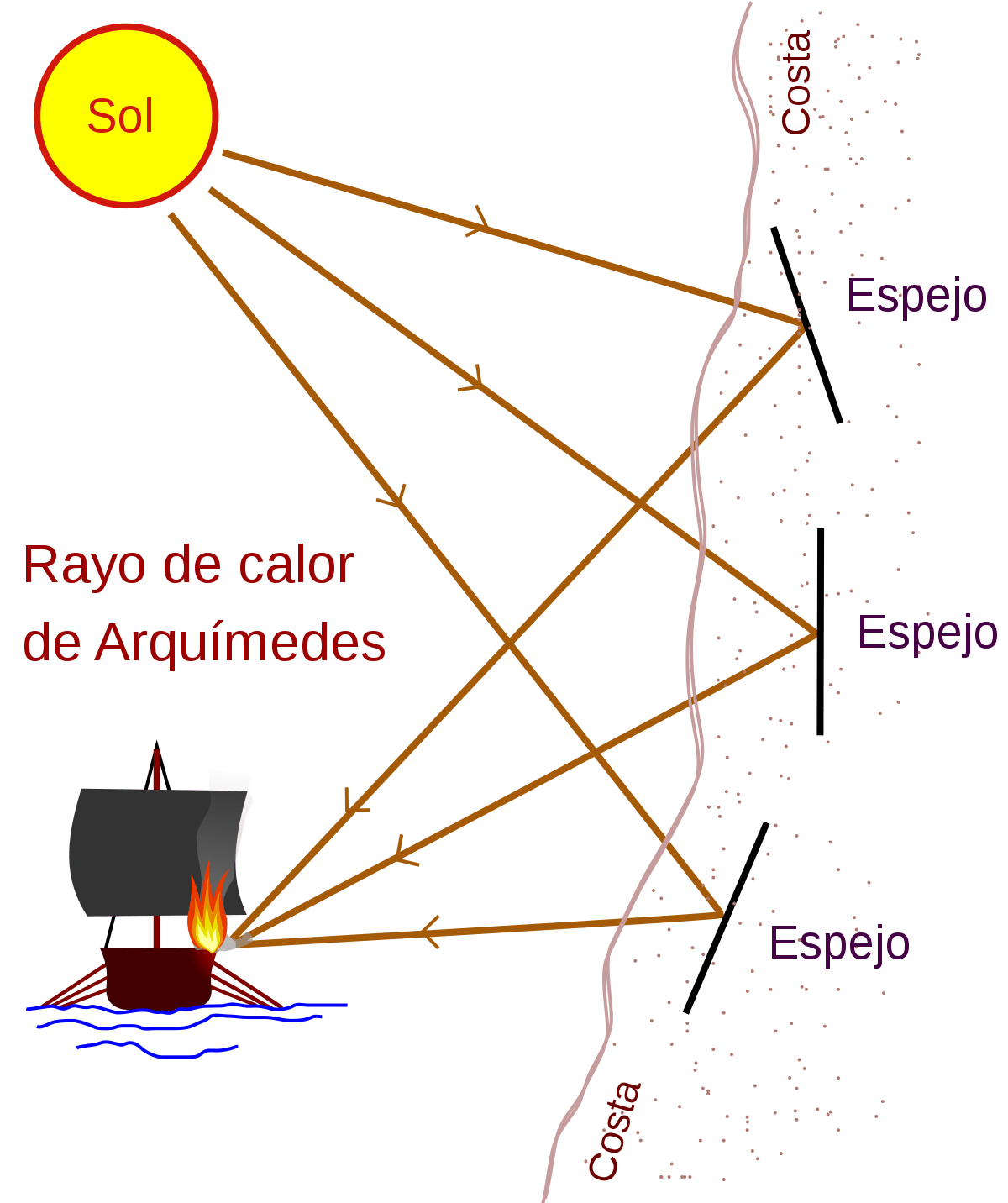
El rayo de Calor también fue un arma de guerra creada por Arquímedes, se trataba de un sistema de espejos según la tradición, dentro de sus trabajos en la defensa de Syracusa, Arquímedes podría haber creado un sistema de espejos ustorios, se tratan de espejos con forma cóncava, los cuales concentran en su foco los rayos solares. Estos grandes espejos eran colocados sobre las murallas de la ciudad y eran dirigidos hacia los barcos enemigos con el propósito de incendiarlos.
Sin embargo, existen muchas fuentes que señalan esta invención de Arquímedes con fechas muy tardías para el momento de su invención, por lo que se ciernen sobre el invento del rayo de calor muchas dudas, no en el hecho de su invención y posibilidad de funcionabilidad, sino en el sentido de que la misma haya sido utilizada como arma de guerra y que además la misma tuviera los resultados esperados.
Dentro de los que señalan sobre el rayo de calor como arma de guerra se encuentran Galeno en el siglo II, Luciano de Samosata también del siglo II y unos siglos después también existen fuentes que señalan el uso de los espejos ustorios como armas de guerra, entre ellos, se encuentran Antemio de Tralles.
Uno de los que rechazan la probabilidad de que el rayo de calor de Arquímedes fuera utilizado como un arma de guerra es René Descartes, matemático, físico y filósofo, Francés. En la actualidad se han realizado algunas pruebas para comprobar la efectividad de la misma, encontrando que deben existir ciertas condiciones para que funcione, dejando un poco entredicho la eficiencia de la misma.
Se dice que para la época es posible que fueran utilizados los escudos de bronce y cobre pulidos, esto asemejaría el principio del reflector parabólico. Por su parte, Georges Louis Leclerc, conocido como conde de Buffon, quien era matemático, naturalista, botánico, biólogo, cosmólogo y escritor Francés, sí creía en que el rayo de Calor de Arquímedes podía funcionar.
Para comprobarlo realizó una prueba en el año 1.747 en los jardines reales, para lo que utilizó más de 150 espejos planos, con los que logro hacer arder una pila de madera ubicada a unos 60 metros. Georges Louis Leclerc, comprobó que era factible hacer arder un barco, señalando una distancia no mayor de 40 metros, para que fuera realmente efectiva como arma de guerra.
A finales del siglo XIX, se realizó la prueba en una base naval en Atenas, el experimento fue coordinado y dirigido por Loannis Sakkas, un científico Griego. En esta oportunidad utilizó 70 espejos, cubiertos con una capa de cobre y con una dimensión de 1,5 metro de alto y 1 metro de ancho.
Este grupo de espejos fueron dirigidos a una maqueta de un barco de Guerra Romano, el cual se encontraba ubicado a 50 metros de los espejos. El barco ardió en llamas en cuestión de unos pocos segundos, sin embargo, se pone en entredicho los resultados obtenidos, debido a que la maqueta estaba pintada, por lo que señalan que es posible que la pintura haya contribuido con la combustión del barco.
Otra variante de comprobación del polémico invento de Arquímedes, fue realizado por un grupo de estudiantes, éstos utilizaron 127 espejos cuadrados de 30 centímetros, los mismos fueron dirigidos a una maqueta de madera de un barco ubicado a 30 metros. Para el momento del experimento el cielo se encontraba nublado y solo obtuvieron resultado cuando el cielo se despejo y debieron mantener enfocado el objetivo por más de diez minutos.
Cuando analizan todas las pruebas y condiciones necesarias que deben estar presentes para que sea un arma de guerra efectiva, se puede concluir que deben estar presentes factores como una excelente reflexión de la luz, una distancia adecuada, un cielo despejado. Por lo que con toda seguridad se podían obtener mejores resultados como arma de guerra, el lanzamiento de flechas en llamas y el uso de catapultas.
Matemática
Lo que más hizo popular a Arquímedes indiscutiblemente fueron sus increíbles y útiles inventos, sin embargo, no podemos dejar de comentar las aportaciones de Arquímedes en el área de la matemática. Arquímedes fue el que consiguió el valor aproximado de Pi (π).
Como sabemos π es un número irracional y una de las constantes matemáticas más importante y mayormente utilizadas, no solo en matemáticas sino en física en la ingeniería y otras áreas del conocimiento. Para lograr esta aproximación Arquímedes utilizó el método exhaustivo y tal como su nombre lo indica, es un método que permite cada vez que se aplica acercarse al valor real.
Solo imaginen la dedicación, paciencia para lograr tamaña aproximación. Arquímedes también hacia uso de los valores infinitesimales, actualmente este tipo de situaciones matemáticas son resueltas con la utilización de las integrales, pero Arquímedes logra obtener resultados en los que incluso una calculadora actual colapsaría. Los resultados obtenidos a través del método de reducción al absurdo, lograba resultados extremadamente precisos.
Es de nuestro conocimiento que π es la relación que existe entre la longitud de una circunferencia y su diámetro, en geometría euclidiana (estudios de propiedades geométricas), Arquímedes para obtener su valor lo más aproximado posible, hizo uso de lo que mejor resultado le daba, sus dibujos.
Entonces dibujó un polígono regular inscrito, es decir, todos los vértices eran puntos de la circunferencia y todos sus lados están incluidos dentro del círculo. También dibujo un polígono circunscrito a la misma circunferencia, es decir, que éste pasaba por todos los vértices del polígono y contenía completamente a la figura en su interior. De esta manera la longitud de la circunferencia y el área del círculo quedan acotadas por esos mismos valores de las longitudes y las áreas de los dos polígonos.
¿Y por qué utilizó esta genial figura?, porque a medida que se incrementa el número de lados del polígono la diferencia se acorta, y de esta manera se obtiene una aproximación más exacta. Por lo que iniciando con polígonos de 96 lados cada uno, Arquímedes calculó que el valor de π debía encontrarse entre 310⁄71 , es decir aproximadamente 3,1408 y 31⁄7 aproximadamente 3,1429, lo cual es impresionantemente consistente con el valor real de π.
Otra de las aportaciones de Arquímedes fue demostrar que el área del círculo era igual a π multiplicado por el cuadrado del radio del círculo. Existe una obra de Arquímedes titulada Sobre la esfera y el cilindro, en la que se encuentra la propiedad arquimediana de los números reales, la cual señala que cualquier magnitud, sumada a sí misma puede exceder cualquier otra magnitud dada, si se suma el número de veces necesarias.
Existen resultados alcanzados por Arquímedes que de manera sorprende son tan exactos a los que se han obtenido en nuestra época, que pueden dejar sin aliento a cualquier erudito de las matemáticas. Uno de estos resultados es el obtenido para la raíz cuadrada de 3, este valor es calculado actualmente como 1,7320508 y Arquímedes dijo que se encontraba entre 1,7320261 y 1,7320512. Lamentablemente no se ha encontrado ningún documento que explique cómo llego a este increíble y exacto resultado.
También desarrollo una serie geométrica infinita, la cual tiene como razón común ¼, esta se encuentra en su obra la cuadratura de la parábola, en la cual explica y comprueba que el área que define una parábola y una línea recta equivale exactamente a un 4/3.
Otro aporte matemático fue la utilización de números enormes escrito de manera exponencial. La inquietud que lo llevo a esta propuesta de un sistema para definir la potencia de un número, fue calcular la cantidad de granos de arenas que caben en el universo. Para ello entonces utilizó la miríada que tenía para la época un valor de 10.000 y señalo que la cantidad de granos de arena que se necesitaban era de 8 x 1063 miriadas (cantidad imposible de calcular). De esta manera dio paso al sistema exponencial.
Escritos de Arquímedes
Las obras escritas por Arquímedes son evidentemente de valor incalculable. En el año 1.906 un filólogo Danés descubrió un compendio de los textos de Arquímedes que permitieron conocer de los procedimientos utilizados por este gran prodigio.
Las obras de Arquímedes fueron originalmente escritas en Griego dórico, que era el dialecto utilizado en la antigua Syracusa. Lamentablemente los textos y escritos de Arquímedes no se ha conservado bien y es una pérdida enorme para la humanidad, ya que se conoce que textos más antiguos, por ejemplo los escrito de Euclides, si se encuentran en mejores condiciones.
Existen también muchos de sus tratados que son conocidos, porque sean hecho referencias de ellas. Dentro de los autores que escribieron sobre los tratados de Arquímedes se encuentra Pappus de Alejandría, gracias a él y su documentación se conoce sobre las esferas y los poliedros de Arquímedes.
Se conoce que al contrario de muchos estudiosos y científicos que ocultaban su trabajo y hallazgos para que no les fueran robadas sus invenciones, Arquímedes las compartía. Es así que se dice que Arquímedes enviaba sus resultados y hallazgos a través de cartas, ya que mantenía una comunicación cercana con los matemáticos de Alejandría. Muchos de los escritos de Arquímedes fueron recuperados en el año 530 después de Cristo por el arquitecto bizantino Isidoro de Mileto.
Algunos de los trabajos de Arquímedes que lograron ser recuperados fueron traducidos al árabe por Thábit ibn Qurra y al latín por Gerardo de Cremona años después. Algunos de los trabajo conservados de este increíble genio matemático se encuentra el de la famosa palanca.
Se dice y se mantiene como frase célebre cuando Arquímedes dijo: “Denme un punto de apoyo y moveré el mundo”, ahora un poco modificado normalmente decimos denme una palanca y moveré al mundo. En donde está escrito el tratado de la palanca son dos libros un primer libro en el que se encuentran 15 proposiciones con 7 axiomas. Un segundo libro con 10 proposiciones y la famosa ley de la palanca.
Arquímedes usa los principios derivados y con ellos logra calcular las áreas y los centros de gravedad de los triángulos, paralelogramos y parábolas. Cada uno de sus escritos es una verdadera obra maestra y comentaremos sobre alguno de ellos a continuación.
La obra que indica cómo hacer la medida de un círculo, es un de las más cortas escritas por Arquímides, esta obra consta de 3 proposiciones. Son cartas que envío a un alumno de Conón de Samos. Es en este documento en el que muestra el valor del número π (Pi) por supuesto en una cifra aproximada. También se logró recuperar el escrito sobre los espirales, este libro está conformado por 28 proposiciones, también dirigido a su alumno Dositeo.
Hoy en día es reconocido este tratado como “La espiral de Arquímedes”. El documento donde habla sobre la esfera y el cilindro, también un documento que había enviado a su alumno, en el que Arquímedes llega a la conclusión matemática de la que estaría más orgulloso, esto es, la relación entre una esfera y un cilindro circunscrito con la misma altura y diámetro.
Este es uno de los enunciados con los que mejor se sintió Arquímedes, señala que la esfera tiene un área y un volumen equivalentes a dos tercios de los del cilindro. Tan orgulloso estaba de haber llegado a esta increíble conclusión, que en vida solicitó que en su tumba colocaran unas esculturas con ambas formas geométricas.
Sobre los conoides y esferoides, podemos señalar que se trata de un documento que contiene 32 proposiciones, en donde se muestran los cálculos de los volúmenes de las esferas, conos y paraboloides. En referencia a los cuerpos flotantes, desarrolla la ley del equilibrio de los líquidos y comprueba la forma que asume un líquido alrededor de un centro de gravedad.
Es en este documento donde indica que todo cuerpo que sea sumergido en un líquido va a experimentar una fuerza que lo empuja hacia arriba y esta será igual al peso de líquido que ha sido desplazado. La cuadratura de la parábola es un trabajo que contiene 24 proposiciones en donde se encuentra la manera como alcanzo Arquímedes el resultado por dos métodos distintos del área de una parábola y una línea recta es 4/3 multiplicado por el área de un triángulo que tiene una base y una altura igual.
Dentro de la compilación de trabajos de Arquímedes llamada Palimpsesto, se encuentra una obra llamada Ostomachion. Esta es una de las obras más completas que existen de Arquímedes en la que muestra el cálculo de 14 partes que al ser ensambladas formaban un cuadrado. En una investigación realizada en la universidad de Stanford señalan que se trata de un ejemplo temprano de un problema de combinaciones. Es un rompecabezas que también es conocido como la caja de Arquímedes.
La vida de Arquímedes giraba en torno a sus invenciones, las cuales siempre tenían un propósito práctico que fuera en beneficio de su ciudad y la manera de divertirse al parecer era retar la sabiduría de sus iguales en Alejandría, es así que se conoce sobre el problema del ganado creado por Arquímides, en el cual reta a Eratóstenes a contabilizar el número de reses en la Manda del Sol, para lo que debían resolver una serie de ecuaciones con más de dos incógnitas, conocidas como ecuaciones diofánticas. Vaya manera de divertirse.
Otra de las obras reconocidas de Arquímedes es el contador de arena, el cual comentamos con anterioridad, en el que calculo cuantos granos de arena podrían llenar el universo. En este documento también se reconocen las aportaciones de Arquímedes a la astronomía, en donde menciona la teoría heliocéntrica, la cual había sido propuesta por Aristarco de Samos.
Entre otras ideas contemporáneas acerca del tamaño de la Tierra y las distancias de varios cuerpos celestes. El contador de arena o Psammites es la única obra de Arquímedes que sobrevive en la que se trata su visión de la astronomía.
También dentro del Palimpsesto de Arquímedes se encuentra el teorema en el que Arquímedes emplea el cálculo infinitesimal, en el que muestra el método de fraccionar una figura, el cual permite calcular su área o volumen. También se encuentra en este documento el método exhaustivo.
Existen también unas obras consideradas apócrifas, como el Libro de Lemmas o Liber Assumptorum en el cual hay 15 proposiciones, sin embargo, varios estudiosos dudan de su autenticidad. Se plantea que tiene versiones de documentos de Arquímedes, pero señalan que no toda la obra es de él.
Reconocimientos
Creo que las aportaciones de Arquímedes fueron tantas y de tal importancia que nunca serán suficientes los reconocimientos que se hagan a este genio de la matemática, astronomía, física, ingeniería e increíble inventor.
Como reconocimiento se le dio su nombre a un cráter lunar que se encuentra en zona oriental de la Luna, conocida como el Mare Imbrium. También hay otra zona en la luna conocida como la cordillera lunar, a la cual le dieron el nombre de los “Montes de Arquímedes”. El asteroide 3600 también lo llamaron Arquímedes en honor al increíble genio.
Existe un galardón que se otorga a los estudiosos e investigadores más destacados en la ciencia de las matemáticas, es llamado La Medalla Fields, esta medalla tiene el retrato de Arquímedes, junto con la relación matemática desarrollada por Arquímedes de las áreas y volúmenes de la esfera y el cilindro.
Otro detalle de este increíble galardón tiene la inscripción de una cita que se atribuye a Arquímedes que dice en latín “Transire suum pectus mundoque potiri” y que significa en español “Superarse uno mismo y dominar el mundo”.
Otra manera que el mundo ha encontrado de hacer un reconocimiento a Arquímedes es la edición de estampillas o sellos, los cuales indicaremos los países y años en los que se han editado, el primero fue España en el año 1.963, luego diez años más tarde Alemania del Este.
Luego Grecia e Italia en el año 1.983, en el año 1.971 realizó una emisión de estampillas Nicaragua y San Marino en el año 1.982. California asume la exclamación “Eureka” como lema del estado, recordemos que la misma es una expresión que se le atribuye a Arquímedes.
Si este artículo ha sido de su agrado, lo invitamos a continuar la lectura sobre grandes personajes de la historia en los siguientes enlaces que le recomendamos a continuación: