Los puntos de Lagrange, también son conocidos como puntos L o simplemente como puntos de libración, se trata de las cinco posiciones que forman parte de un sistema orbital. En el siguiente artículo conoceremos más de los puntos lagrange y cada uno de sus procesos.
Indice De Contenidos
Puntos de Lagrange
Los puntos de Lagrange, reciben también las siguientes denominaciones:
- Puntos L
- Puntos de libración
Son catalogados como las cinco posiciones dentro de un sistema orbital donde generalmente un objeto pequeño, sólo afectado por la gravedad, puede presentarse teóricamente estacionario con relación a dos objetos que sean más grandes, en este sentido abarca la comparación de un satélite artificial con respecto a la Tierra y la Luna.
Los llamados puntos de Lagrange, suelen trazar las posiciones donde reflejan que la atracción gravitatoria muestra una combinación de las dos masas grandes, las cuales proporcionan la fuerza centrípeta que a su vez es requerida para que se pueda rotar de forma sincrónica con la que se presenta como menor en ellas. Son clasificadas como análogos a las órbitas geosincrónicas, y ayudan a un objeto a mantenerse en una posición (fija), en el espacio en lugar de en una órbita en la cual su posición se muestra relativa y genera cambios de manera continua.
De una manera más específica, pero en un toque técnico se considera que los puntos de Lagrange, son las soluciones de forma estacionarias del conflicto presentado correspondientes a los tres cuerpos restringido a las órbitas circulares.
Historia
Los antecedentes históricos muestran que en el año de 1772, se realizaron ciertas investigaciones por parte del matemático, conocido como Joseph-Louis Lagrange, en esta ocasión se encontraba trabajando en el ilustre problema de los tres cuerpos cuando descubrió un interesante aspecto, debido a que buscaba la manera sencilla de calcular la interacción gravitatoria de un número arbitrario de cuerpos en un sistema.
Debido a que la mecánica newtoniana, suele determinar que un sistema con este tipo de características gira caóticamente hasta que se produzca una colisión, o simplemente alguno de los cuerpos sea expulsado del sistema y de esta forma se obtiene el equilibrio mecánico.
Aunque, si se introduce un tercer cuerpo, o más, los cálculos matemáticos se vuelven algo complejo. En este caso se tendría que calcular la suma de todas las interacciones gravitatorias basados sobre cada objeto en cada punto específicamente a lo largo de su trayectoria.
Sin embargo, en sus estudios Lagrange quería plantear una forma más fácil, y gracias a las investigaciones realizadas logró hacer un enfoque exacto de su punto de vista mediante una simple hipótesis: La cual estaba basada en la trayectoria de un objeto que se determina localizando un camino que minimice la acción con el tiempo.
A través de ese enfoque, se calcula sustrayendo la energía potencial de la energía cinética. Dicho planteamiento, establecido por Lagrange, causó un efecto significativo, ya que reformuló la mecánica clásica de Isaac Newton para dar paso a la mecánica denominada como lagrangiana. Con esta nueva forma de calcular, el trabajo de Lagrange le permitió plantear la hipótesis de un tercer cuerpo de masa despreciable en órbita alrededor de dos cuerpos más grandes que ya estuvieran girando a su vez en órbita cuasi circular, dicho enfoque sirvió para dar más fuerza a su opinión.
Por lo general en un sistema de referencia, que se caracteriza por girar con los cuerpos mayores, se ubican cinco puntos fijos, los cuales son específicos en este sentido los que pertenecen al tercer cuerpo, al seguir la órbita de los de mayor masa, se encuentran sometido a fuerza cero. Estos puntos fueron catalogados como puntos de Lagrange en honor a su gran aporte.
A nivel general, en cuanto a las órbitas elípticas no existe ya puntos estacionarios sino que más bien se trata de un “área” de Lagrange. Los puntos de Lagrange son catalogados como sucesivos, considerando órbitas circulares en cada momento, también forman órbitas elípticas estacionarias, que resultan geométricamente similares a la órbita de los cuerpos mayores.
Este hecho se establece como consecuencia de la segunda ley de Newton, la cual se establece de una manera concreta dónde p = mv (p es la cantidad de movimiento, m la masa y v la velocidad). en este sentido p es considerada como un invariante si la fuerza y posición se multiplican por un mismo factor.
De esta forma, un cuerpo en un punto de Lagrange órbita en el mismo período, establecido en los dos cuerpos grandes en el caso circular, de esta manera presentan la misma proporción entre fuerza gravitatoria y distancia radial. Este hecho se muestra independiente de la circularidad de las órbitas e implica que las órbitas elípticas sean descritas por medio de los puntos de Lagrange, los cuales son establecidos como soluciones de la ecuación de movimiento del tercer cuerpo.
Los puntos de Lagrange
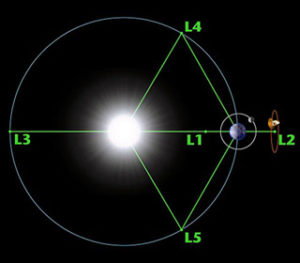
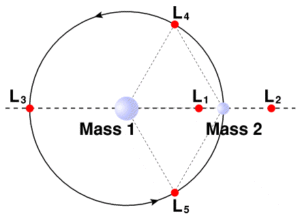
Generalmente el diagrama que muestra los cinco puntos de Lagrange, establecidos en un sistema de dos-cuerpos de masa suelen ser muy diferentes (por ejemplo el Sol y la Tierra). En este sentido, en un sistema así, los puntos catalogados como L3–L5 suelen hacer la similitud de que giran en la misma órbita que el cuerpo segundo, aunque se puede apreciar que lo hace ligeramente más alejado del primero.
- En cuanto a los cinco puntos lagrangianos se denominan y se definen de la siguiente manera:
El punto L1
El punto L1, se encuentra establecido entre las dos masas grandes catalogadas como M1 y M2 en la recta que las une. Suele mostrarse de como más intuitivo de los puntos de Lagrange: basados en aquel en que las atracciones opuestas de los dos cuerpos mayores se compensan.
- Ejemplo: un objeto que realice un proceso donde orbite alrededor del Sol más cerca que la Tierra tiende a presentar un período orbital que resulta más corto que la Tierra, aunque esto ignora por completo el efecto de atracción gravitatoria de la Tierra.
- En este caso si, el objeto está se localiza de manera directa entre la Tierra y el Sol, entonces el efecto de la gravedad de la Tierra será debilitar la fuerza que tira del objeto hacia el Sol, por tal motivo, se genera un aumento en el período orbital del objeto. Debido a que más cerca está el objeto de la Tierra, mayor es este efecto.
El punto L2
El punto L2, está establecido en la línea que se encuentra definida por las dos masas grandes consideradas como M1 y M2, y más allá de la más pequeña de las dos. En él se refleja la atracción gravitatoria de los dos cuerpos mayores en este caso se compensa la fuerza centrífuga ocasionada por el menor
- Ejemplo: un objeto que específicamente orbite el Sol más lejos que la Tierra mostrara un período orbital considerado como más largo que el de la Tierra. Debido a que la fuerza adicional de la gravedad de la Tierra logra disminuir el período orbital del objeto, en este sentido el punto L2 es aquel en que el período orbital es igual o similar al de la Tierra.
El punto L3
El punto L3, se encuentra establecido en la línea definida por las dos masas grandes, catalogadas como M1 y M2, y más allá de la mayor de las dos.
- Ejemplo: el punto L3 en el sistema de Sol–Tierra está en el lado opuesto del Sol, un poco más cerca del Sol que la propia Tierra. Esta aparente contradicción, recibe una explicación basada en que el Sol está también afectado por la gravedad terrestre, y por tal motivo gira en torno al centro de masas común o baricentro que, no obstante, se encuentra localizado dentro del Sol. En L3 la fuerza gravitatoria combinada de la Tierra y del Sol ocasiona que el objeto orbite por medio de un proceso determinado, ya que lo hace con el mismo período que la Tierra.
Se ha determinado, que la L3 en el sistema Sol-Tierra suele mostrarse muy inestable, debido a las fuerzas gravitatorias de los demás planetas que pueden llegar a superar a la de la Tierra, ( como es el caso de Venus, ya que por ejemplo, pasa en un indice de 0.3 AU de L3 cada 20 meses).
El punto L4 y el L5
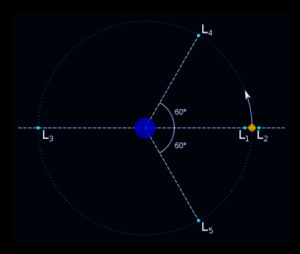
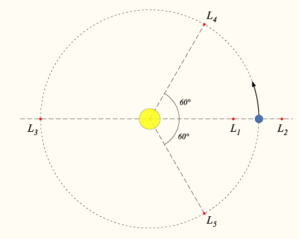
En cuanto al punto L4 y el punto L5, están establecidos en los vértices de triángulos equiláteros cuya base común es la recta que une las dos masas, esta manera el punto L4 se muestra al cuerpo por medio de un pequeño un ángulo de 60º, observado desde la masa grande, mientras que L5, realiza otro proceso, este gira detrás del cuerpo pequeño, aunque lo hace con radio mayor que éste, presentando un retraso de 60º visto a su vez desde el cuerpo grande.
Dichos puntos, al igual que sucede con el cuerpo menor de masa M2, no giran sobre el cuerpo grande, sino que realizan otro proceso moviéndose sobre el baricentro de ambos cuerpos marcado como b en la figura.
En el caso del cuerpo grande también suele girar sobre b con un radio r1, en este sentido el radio r de la órbita común a los puntos catalogados como L4 y L5 puede deducirse por medio de la figura mediante razonamientos geométricos:
Considerando así que los radios de las órbitas pertenecientes a los cuerpos grandes considerados como r1 y r2 están en relación inversa de sus masas: en este caso se resuelve el triángulo formado por L4, b y el centro de masa del cuerpo menor; establecido en la relación.